
Dopo aver trattato le bellicose questioni su DPI e PPI, daremo una risposta che dovrebbe mettere d’accordo tutti.
Questi tipici interrogativi legati al rapporto dimensioni/risoluzione magari si risolvono comprando sempre quella più grande così si limitano i danni (e si spende in modo sconsiderato), ma dal momento che nessuno sano di mente cuoce mezzo kg di pasta se deve mangiarne 1 hg, tanto vale capire cosa serve e perché.
Prima di tutto cerchiamo di circoscrivere meglio l’interrogativo, dato che così è malposto: che valore di risoluzione di Output è opportuno usare (o che dimensioni in pixel è opportuno avere) per una data immagine X che debba essere vista a una distanza minima Y e che venga stampata/visualizzata su un dato supporto Z?
X,Y e Z sono le tre incognite che, una volta correttamente identificate, ci faranno arrivare a una soluzione soddisfacente.
Una doverosa premessa: quanto segue pone l’accento più sulla struttura logica che sulla precisione matematica, non me ne vogliano quindi i puristi o i super tecnici, la rete offre diverse trattazioni molto approfondite a riguardo e considerando l’ambito grafico in cui ci muoviamo in questa sede tali approfondimenti sono decisamente «troppo» e senza alcun valore aggiunto finale. La trattazione più completa di cui io sia a conoscenza potete trovarla nel libro Misurare il Colore del Prof. Claudio Oleari (attenzione! Perché richiede solide basi di matematica e non solo!)
X, Y, Z sono le tre variabili che, una volta identificate correttamente, ci porteranno a una risoluzione soddisfacente.
L’immagine X
Riassumendo, le immagini con molti dettagli sottili (microdettaglio o alte frequenze se preferite) richiedono più attenzione delle immagini con prevalenza di volumi (o basse frequenza). Forti contrasti sulle piccole dimensioni evidenzierebbero subito eventuali aliasing (seghettature) da pixel «troppo» grandi, motivo per cui la valutazione della risoluzione ottimale non può prescindere dal soggetto presente sulla foto.
In base a questa premessa ricordiamoci quindi che il valore di risoluzione ottimale, che andremo a calcolare nel corso di questo articolo, potrà essere ragionevolmente aumentato di circa un 10-15% in presenza di immagini con molto microdettaglio, o ragionevolmente ridotto di pari percentuale per immagini con poco o nullo microdettaglio.
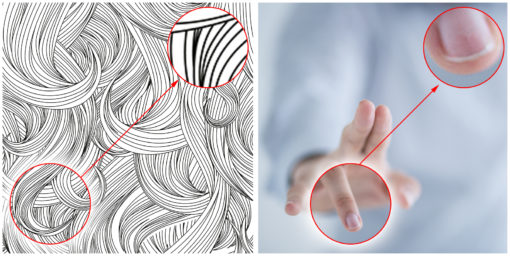
A fronte di un medesimo fattore di ingrandimento (400%) i pixel nativi non sono sufficienti per una buona resa nell’immagine di sinistra, sono invece accettabili per quella di destra.
Dopo aver calcolato la risoluzione di riferimento in base alle dimensioni fisiche necessarie per questi due casi si dovrà tener conto delle diverse caratteristiche per ritoccare il valore di conseguenza, per esempio considerano una risoluzione limite più alta per quella di sinistra.
La distanza Y
Questo è il discriminante più importante dei tre.
L’occhio umano medio risolve un certo dettaglio, che statisticamente possiamo indicare con buona approssimazione pari all’ampiezza di un arcominuto, cioè un primo di grado, cioè un sessantesimo di grado. Misure molto precise su casi specifici possono essere fatte a partire da:
1 Distanza minima dei fotorecettori nella fovea;
- Usando formule trigonometriche anziché approssimazioni lineari (comefaremo in questa sede)
- Considerando il caso di contrasto massimo offerto da linee alterne bianche enere con illuminazione ottimale;
Tutta questa precisione per noi non ha molto senso, perché:
1 Anche se la distanza minima dei fotorecettori è sostanzialmente uniforme tra i vari individui, le grandezze in gioco sono estremamente piccole, ed eventuali difetti di visione dovuti a miopia, presbiopia, ipermetropia, criticità dovute all’età o alla stanchezza, o alla genetica, o al sesso (le donne sembra siano statisticamente leggermente più sensibili anche in questo contesto) creerebbero variazioni tutt’altro che trascurabili sul risultato preciso dei calcoli.
2 Proprio per le piccole dimensioni in gioco le misure dei segmenti circolari che prenderemo in considerazioni potranno essere tranquillamente approssimate a segmenti lineari con uno scarto irrisorio, a tutto vantaggio dei calcoli da fare senza scomodare la pur più precisa trigonometria (o altro).
3 Le immagini di cui parliamo nel contesto grafico, e in generale tutto il mondo visibile, (emesso, trasmesso o riflesso che sia) offrono una variabilità di fattori di contrasto pressoché infinita, e raramente è solo composta da elementi solo bianchi e neri. Quindi se una serie di linee bianche e nere sottilissime risultano distinguibili, altrettanto non si può dire di un’analoga serie con linee sottilissime verdi/rosse o blu/azzurre ecc…
3 bis. Un conto è riuscire a distinguere perfettamente dei dettagli, un altro è distinguerli quel tanto che basta per mettere in moto i meccanismi percettivi ben delineati dalla Gestalt, sulla base dei quali anche un’identificazione parziale è sufficiente per generare nella nostra mente il contesto completo.
Un classico esempio ce l’abbiamo nella lettura: una volta identificate le lettere chiave di una parola il nostro cervello automaticamente assembla la parola completa e ci permette di scorrere velocemente. A volte questo genera errori di associazione, per esempio con parole che vediamo la prima volta, e quindi ci troviamo a leggere con attenzione le singole lettere finché la parola non risulta acquisita.
Il supporto Z
Il tipo di supporto, non necessariamente carta, così come la tipologia di stampa o di riproduzione video, creano una certa variabilità sulla definizione dei dettagli originari.
Il nostro occhio vede in modo continuo, analogico, ma la quasi totalità dei sistemi di riproduzione è discreta e si basa su retini, dithering e lineature.
Tali combinazione di inchiostri o pixel, associati a supporti più o meno omogenei, permettono al nostro occhio di vedere «bene» l’immagine rappresentata grazie alla sintesi additiva in media spaziale.
Gli esempi di questo sono molteplici:
◗ una foresta da lontano ci sembra circa verde, man mano che ci avviciniamo e riusciamo a distinguere più dettagli possiamo osservare tronchi, alberi, foglie ecc… Le onde luminose riflesse a distanza dalla foresta arrivano al nostro occhio che per quello che riesce ne fa una media e ci restituisce l’informazione «la foresta è verde».
◗ Il retino di stampa visto al lentino è un insieme di punti Cmyk, visto da una certa distanza il nostro occhio ne fa una media e «sintetizza» i vari colori.
◗ Sfumature di grafite su una carta ruvida viste da vicino mettono in evidenza la trama della carta, da una certa distanza invece la combinazione di striature di carta bianca e grafite restituisce nella nostra testa un’idea generale di «sfumatura» continua.
◗ Un videowall gigante, da stadio, visto da vicino presenta grossi elementi luminosi RGB (probabilmente pallini ma non solo), visti dalla curva opposta al nostro occhio arriva invece l’immagine continua.
Gli esempi potrebbero continuare all’infinito. Una volta compreso che queste tre variabili possono interagire e rendere quindi parzialmente interpretabile il risultato numerico finale, andiamo ora a calcolare la risoluzione che ci serve.
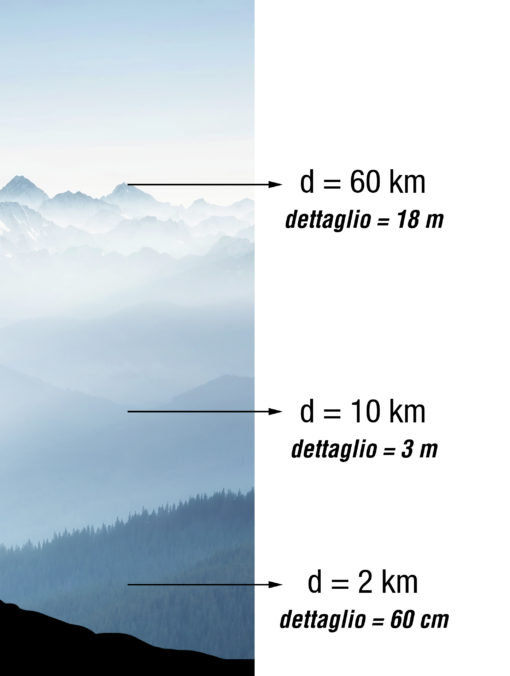
Nell’esempio ho ignorato problematiche reali come l’atmosfera che interferisce non poco con la visioni a distanza.
Il problema della foschia generalmente con le stampe non lo abbiamo…
E allora risolviamo
Assumendo con buona approssimazione che il nostro occhio risolva mediamente un dettaglio ottimale pari a un arcominuto andiamo a calcolare qual è il più piccolo dettaglio che siamo in grado di risolvere alla distanza di 1 metro, con la matematica più spicciola possibile.
Un arcominuto è un primo, cioè un sessantesimo di grado, e in un cerchio i gradi sono 360.
Se poniamo quindi l’osservatore al centro di un ipotetico cerchio di raggio 1 metro è sufficiente sapere la lunghezza di un arco ampio un sessantesimo di grado per avere ciò che cerchiamo.
In ultima analisi, come anticipato prima, il nostro arco lo approssimeremo per semplicità a un tratto lineare. La circonferenza è pari a 2 π r quindi 2×3,14×1=6,28 m.
Dividiamo 6.280 mm (6,28 m) per 360 per trovare la lunghezza di un arco di ampiezza un grado e poi dividiamo ulteriormente per 60 per la lunghezza dell’arco di ampiezza 1 primo.
6.280/360=17,44 mm
17,44/60=0,29 mm
L’ampiezza che ci serve è 0,29 mm, che potremmo tranquillamente assimilare a 0,3 mm.
A un metro di distanza l’occhio umano medio in condizioni di illuminazione e contrasto ottimali risolve un dettaglio pari a 0,3 mm (circa un terzo di millimetro in pratica).
Dato che il più piccolo dettaglio determinato in un’immagine digitale è dato dalla grandezza del singolo pixel che la compone, questo significa che l’immagine vista a un metro di distanza dovrà avere un pixel di riferimento grande non più di 0,3 mm. Se è maggiore di questa dimensione aumenta rapidamente il rischio di percepire aliasing.
Tradotto in Pixel Per Pollice vuol dire trovare quanti pixel da 0,3 mm stanno in un pollice, ossia 2,54 cm, e risulta circa 85 PPI.
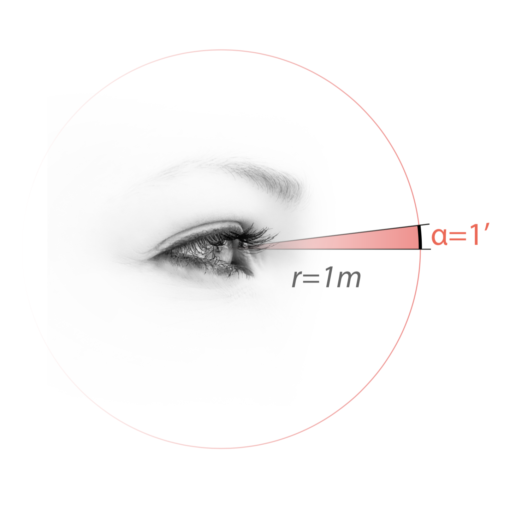
Considerando le piccole dimensioni in gioco possiamo approssimare l’arco a un segmento trascurando lo scarto.
(RI)Soluzione
Per un’immagine che vada vista a un metro di distanza la risoluzione di Output di riferimento è di 85 PPI a dimensioni fisiche reali, da aumentare se l’immagine in questione è ricca di dettagli (magari a 100 PPI), anche 70 ppi se si tratta di un’immagine senza particolari dettagli, come un tramonto.
Le dimensioni fisiche sono secondarie, può trattarsi di una cartolina 13×18 come di un manifesto 100×140 cm, il discriminante è la distanza di osservazione, non la grandezza del supporto. Poi va da sé che è estremamente improbabile che una cartolina sia da guardare da lontano o un manifesto 100×140 sia da guardare molto da vicino, ma questo riguarda la tipologia dell’elaborato grafico e le regole di composizione grafica, secondarie rispetto all’argomento dell’articolo.
Volendo realizzare un cartellone da 6×3 metri andrà più che bene un’immagine da 15 PPI, invece per un stampa fotografica da interni di 2×3 metri a soggetto beauty visibile potenzialmente anche a distanze intorno ai 50 cm non è il caso di scendere sotto ai 150 ppi, sempre a dimensioni reali (e in casi come questo le immagini necessarie avrebbero più di 200 Megapixel…)
Conclusioni ragionate
Una volta compresi i meccanismi di visione che stanno alla base dei processi percettivi possiamo inquadrare problema e soluzione con ottimi risultati. Se serve una formula ancora più spicciola potreste usare questa:
Risoluzione di Output = 80/d,
dove d è la distanza dell’osservatore espressa in metri.
Con un veloce ragionamento possiamo anche trovare una buona motivazione ai classici 300 ppi consigliati per le stampe in alta risoluzione: a una distanza di circa 25-30 cm, tipicamente la distanza media di lettura di riviste o libri, la risoluzione consigliabile risultante sarebbe di 80/0,25 e 80/0,30, i cui risultati danno 320 e 266 PPI.
Come ordine di grandezza direi che ci siamo, no?




